To Do Away with Backprop
Published:
From The Forward-Forward Algorithm: Some Preliminary Investigations, Geoffrey Hinton In this paper, Hinton explains a new forward-forward (FF) algorithm to replace backpropagation.
Summary
Motivation: The success of backprop has led to much debate about weather the real brain learns in the same manner. However, there has been little evidence to support this. For example, the visual pathway. One would expect bottom-up connections from one cortex area to another that precedes it in the visual pathway. Instead, top-down connections that have loops were discovered. Neural activity goes through some cortical layers before returning to its starting point. This makes BPTT quite implausible as a method of learning sequences in the human brain. The brain’s perceptual learning system performs inference and learning in realtime without stopping to compute backprop.
The main point of this paper is to show that neural networks containing unknown non-linearities do not need to resort to reinforcement learning.
The problem with backprop: Backprop requires perfect knowledge of the computation performed in the forward pass or or the differentiable model of the forward pass to compute the derivatives in the backward pass. Backprop cannot take place if the forward pass were a black box computation. This is not an issue for the forward-forward (FF) algorithm.
An RL approach can make up for this shortcoming through random trial and error of weights and correlating the resulting change in a suitable reward function. However, RL models have high variance, especially when there are many changing variables. RL requires the lr to be inversely proportional to the number of variables being ‘guessed’, making RL a method that scales poorly for large networks.
The Forward-Forward Algorithm
The idea is to replace the forward and backward passes of backpropagation by two forward passes that operate in exactly the same way as each other, but on different data and with opposite objectives.
- +ve pass: uses real data, adjusts weights to increase goodness on every hidden layer
- -ve pass: uses -ve data, adjust weights to decrease goodness in every hidden layer
Goodness Function Used: sum of the squares (or -ve squares) of the activities of the rectified linear neurons in that layer
The goodness function was selected due to very simple derivatives and layer normalization removes all trace of the goodness.
Training:
The aim of learning is to make the goodness be well above some threshold for real data and well below the same value for negative data. The model should correctly classify input vectors as +ve or -ve by applying the logistic fn to the goodness, minus some threshold θ.
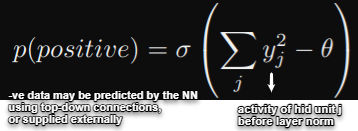 source: research paper linked above
source: research paper linked above
FF normalizes the length of the hidden vector before using it as input to the next layer. This removes the length information of the activity, which defines the goodness for that layer. Only the orientation (relative activity) of the activity will be passed on to the next layer. This is because it is not necessary for the model to learn new features from the length data.
Experimental Setup
Motivating Questions:
- If we have a good source of -ve data, does FF learn effective multi-layer representations that capture the data structure?
- Where does the -ve data come from?
The Method:
Contrastive Supervised Learning Dataset: MNIST Preprocessing Real data –> +ve || Corrupted data –> -ve There are various ways to create corrupted data. Hinton manually creates corrupted -ve data using masks, and focuses on creating data with very different long range correlations but very similar short range correlations. This forces FF to focus on long range correlations in imgs that characterize shape.
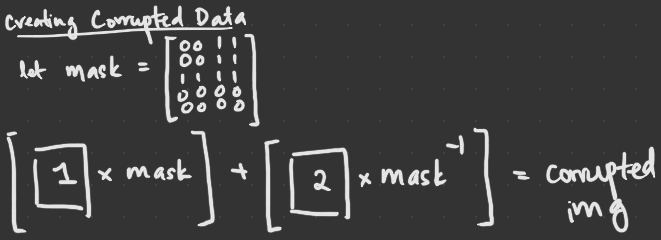 source: i draw things
source: i draw thingsWhen jittering is applied on the data, test error decreased to 0.64% (from 1.36% before), which is close to a backprop cnn. Images were jittered by 2 pixels in each direction to get 25 different shifts for each image. This forces the use of spatial layout of pixels, making the model no longer permutation invariant.
permutation invariance: where a model does not assume spatial relationships between features.
Training
- Learn to transform input vec into representation vec without using info about the labels
- Linear Classifier: Learn simple lin transformation of the rep vec –> logit vec –> softmax to find probability distribution over labels
- Run the net with a particular label as part of the input, and accumulate goodness of all except the first hid layer. Do this for each label separately, then choose the label with the highest goodness.
Key Takeaways
| Backprop (BP) | Forward-forward (FF) |
|---|---|
| Likely here to stay for most general applications | Currently does not generalize that well |
| Outperforms in 2 cases: 1. as a model for cortex learning 2. low-power analog hardware (can replace RL) | |
| Comparable/Slightly slower speed to BP (paper did not clarify if it referred to training or prediction speed) | |
| Can be used when forward pass is unknown | |
| Can learn while pipelining sequential data continuously |
Things to Note:
- The paper only tested FF on small networks of a few million connections. Large networks have yet to be tested.
